The most beautiful puzzle that my engine can never solve

Question: When does Stockfish analyse every move (needed to determine the result)

Answer: Whatever time it needs to analyse the finite number of nodes needed.

It's not difficult (to me). I accept that it's beyond you.

You seem hopelessly confused between the algorithmic truth and what happens when you have a trillion times (or more) too little time to do the analysis.

Do you understand that there are only a finite number of legal positions in chess?

(Lack of answer will be taken as meaning you don't).

I will generously take that as a correct answer: there are indeed merely a finite number of positions in chess.

Next question:

Do you understand that while Stockfish is analysing it is constantly adding more analysed nodes?

[Assume the hash table is big enough so that it never gets full. Eg, big enough for all legal chess positions - impractical, but simple to the algorithm. This makes the answer clearer].

Now I am going for a cycle, but I will be back to see your ego-motivated pot-shot later. But do answer the question too.

You should understand that past a certain depth, no more nodes are added because they are all already there. (It's because the set of legal positions is finite (also there is a finite upper limit on the number of moves in a legal chess game).

So, no. After this depth has been reached , the percentage of moves that have been analysed obviously keeps going up from there. [More simply, the percentage of all legal positions in chess that have been analysed goes up until the analysis is complete].

The final question:

Does the Stockfish algorithm stop when there remain nodes that could affect the overall evaluation that have not been analysed at all?

Jeez. Everyone else can see I am NOT changing the subject.

Please answer the final question if you understand it.

Does the Stockfish algorithm (on "infinite analysis") stop when there remain nodes that could affect the overall evaluation that have not been analysed at all?

[Also, you presented an erroneous argument that the Stockfish algorithm does not analyse all positions that are relevant to a problem. The fact that you have already forgotten this from a few hours ago explains why you stay wrong.].

Again, do you not understand what a question is? Ask someone else to explain my last post to you if you don't.

The answers to the three questions I have asked you (you have got the first two right already) provide most of the proof you desire. There is only one more step once you answer the third question.

The proof is this.

Firstly, 3 simple facts. (You have stated the first two and would be unwise to dispute the third).

1. There are a finite number of positions

2. While the Stockfish algorithm is doing analysis it is continually adding new positions to the analysis tree

3. The Stockfish algorithm will not stop if it has sufficient computational resources and there is an position that has not been analysed and can be relevant.

Then one deduction (you should be able to understand this. If not the answer is to get able to do so).

Conclusion: given unlimited computing resources, the Stockfish algorithm finds the very best line.

This is an impractical result because most chess positions would take (much) more than a million years to solve using Stockfish on a fast computer, even one enhanced with the stupendous amount of memory to store a huge analysis tree. Experts are likely to have told you what happens in reasonable time. It's irrelevant what it could do in billions of years (but it is relevant to our question).

You are wise not to have been following.

But you have gone straight to the crux. A ridiculously large amount of time is not the same as an infinite amount of time.

While it is not logically impossible that Stockfish has code such that there is some evaluation of a position in a tree that means it will never look at it regardless of whether there are no other leaf nodes remaining, I don't believe this is plausible. It can certainly solve puzzles where a couple of queen sacrifices are necessary and that sort of thing. There would be no point in having a line drawn for when it is 3 queens down, or whatever. A move can be ignored if another move leads to a forced mate (although we probably all know (like I do) that Stockfish often updates its belief about the number of moves to mate, finding a long mate first, then finding a faster mate later, so it does not do this).

I am not sure that @DesperateKingWalk understands that "never in a million years" is not the same as "never".

No.

[And your reading comprehension is poor].

Do I need to tell you a third time that chess has a finite number of legal positions?

The answer to your question "does it?" is "yes, it does".

The only thing that stops Stockfish looking at every move is computational resources, especially TIME.

On multiple occasions you have forgotten that all the empirical evidence involves a minuscule amount of time. We are discussing what the algorithm would do with unlimited time and space. (The fact that it can't solve some problems with practical time has never been in question).

Let's see what Stockfish does when it is in a position to eliminate every node except one, but still has time to analyse. The answer is that it continues to analyse DEFINITELY INFERIOR BRANCHES. Given that, the belief that it might ever PERMANENTLY ignore branches that COULD BE BEST is ridiculous.

I don't know what StockFish currently does and how. But I do know I would program every chess engine - and I would be massively surprised if it isn't done already - to have a thread (threads) running doing a full tree search on the chance it strikes gold. Even if just running in the background as a garbage collector on 1% of CPU-time. When quantum computing gets fast enough (assuming it can) I would delete all the other code. The point is that there is a balance between the required complexity of the software and CPU speed plus memory. In the last century russian infomation theorists were considered brilliant in designing algorithms which they needed for instance in their space rockets since their computers were slow compared to those in the west.

Your skillset appears to mostly consist of glibly repeating vague mantras and being abusive. Also incorrectly reasoning from quotes.

The skill you could do with developing is logical reasoning.

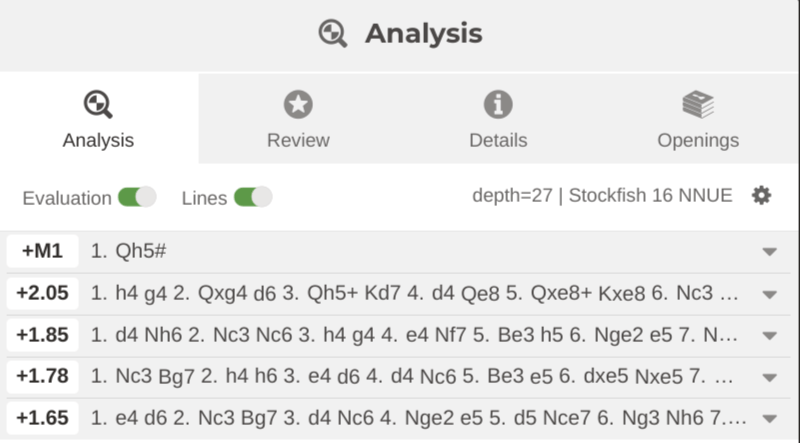
You don't seem to understand what a 1-ply analysis is. The position I posted showed analysis lines to many moves and a search depth of 26. That is NOT a 1 ply analysis. Note also, that you seem to forget that a 1-ply analysis generates a new set of positions without 1-ply analysis. At the extremes of an incomplete analysis tree, you always have a set of positions that do not have a 1-ply analysis. If every position has a 1-ply analysis, the analysis is complete, contrary to your fanatical belief.

The point was that the lines Stockfish was analysing in my example were the most extreme example of irrelevant, inferior lines possible. The idea that it would fail to permanently prune such lines but prune some other type of line is, to an intelligent person, obviously absurd.

One possibility you miss is that Stockfish can do its analysis, pruning low priority (or even strictly inferior, like in my example) lines, but later, when there is nothing better to do analyse those lines. That is what happens in my example, and that is what happens at every leaf node in the hypothetical end.

It is an interesting discovery that Stockfish does this even when it has categorically solved a problem - it has found the shortest mate, proved that there are no other alternative mates, and yet continues to analyse inferior lines. Because it can, and it has nothing better to do.

In our hypothetical case where Stockfish has no problems with computational resources, it does the same at every position in the analysis tree, each one being in the hash table so it is found if it is reached by transposition.

No, that is an answer a google search finds on Quora. It is from a contributor using the fake name "Alfred Alphazero". But it is correct if about a specific implementation of Stockfish, which can have say a maximum hash table size. Here is a more relevant answer from someone who uses his real name.

I want to learn more!

Whatever StockFish does or can do (are they different?) the underlying design principle is that reaching an end point (in time) has a higher priority than reaching an end position (game state). The point where SF could solve chess has long been passed because the price was too high - 200 billion years. Which is the fate of complex mathematics. You won't see it appear until it has been reduced and restricted and the tools are powerful enough to permit practical application - see ChatGPT.

Yes. There is a huge gap between the theoretical and the practical.

With AI, it wasn't so much that there was a theoretical demand, it's just that enormously increased computational power made a lot more possible. I was fascinated by neural networks in the dark ages (after they had been invented then went out of fashion while computationally cheaper alternatives had a lot of success. With 1000 times more computing resource (probably a million times with the big LLMs, which run on very powerful centralised hardware with stacks of state of the art TPUs), a lot more has been achieved.

The ChatGPT hardware has thousands of individual units suitable for interacting with individual users, each of which has 8 state of the art V100 TPUs. Each of those units is more powerful than the world's fastest supercomputer in 2004 - 800 teraflops.

If white moves first my engine took 10 seconds and depth 42 to realise white is winning